My first class of CUDA programming was almost a nightmare ( I have fortunately enrolled spontaneously). I was excited to learn about GPGPU and was expecting to do some really cool stuff on GeForce cards within that semester. The truth however was, that we have spent quite a long time in CPU assembly (SSE Instructions) and also with CPU Threads and their synchronization and work distribution. Only half of it was dedicated to CUDA programming itself and what was left was already interlaced with OpenGL graphics – I haven’t successfully finished this class to be honest.
One of my first tasks as a CUDA beginner was to properly implement this simple algorithm and I have really struggled with it. The performance was very poor and there was a lot of small data-copy tasks, which are extremely inefficient. Basically it was almost as horrible as myself implementing soon after the FFT R2 radix in polar coordinates ? – Ya, never do that – always make sure to copy as much data as possible within a single data-copy call and think twice whether you really need to use sin() / cos() functions, as those are quite expensive and can be under some circumstances precomputed ahead just as a simple LUT (Look-Up-Table) – which can be – due to the nature of graphics cards- really fast. Remember that fetching static memory is one of the most common tasks a GPU can do (Fetching textures for video games) ? Besides, there is this 64KB constant memory available in CUDA – Google it!
Okay, lets see what this post is about – basically we will implement a Matlab’s function “cumsum()” – a cumulative sum of a vector where each data element is the sum of its previous values. From the definition I just mentioned, every C/C++ beginner is able to code this algorithm properly. For CUDA, we will however choose the Hillis & Steel algorithm, which works in a slightly different fashion. So first of all, CPU has a linear complexity of work O(N), this “parallel prefix sum” has only O(log(n)), so it will run faster, the flow (for N = 8) is shown below:
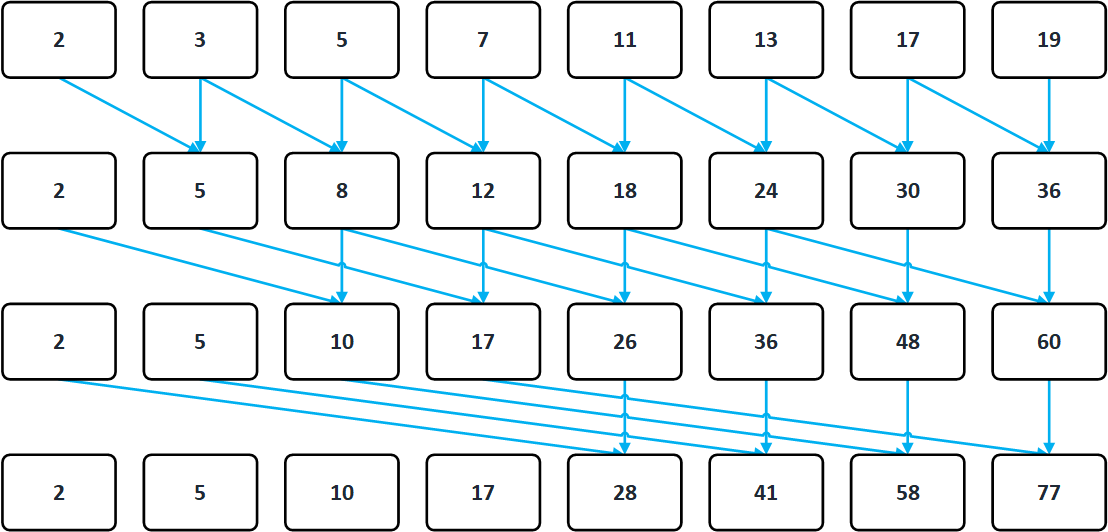
What is important to note by looking at the scheme – And that is a very common mistake! – is that during computation of a phase, you need to make sure that writes and reads are synchronized – IE updating the same array will lead to errors more importantly in a massively parallel environment such as in CUDA! In order to overcome this, we introduce memory barriers – but don’t worry, it is very simple, just make sure, that you are reading from a different buffer than you are writing to and that’s it. Problem solved ? See below naive Kernel for details:
/********************************************************
* @brief: Implementas Parallel Prefix Sum (Hillis-Steel)
********************************************************/
__global__ void Steel_Default(int *Input,int*Output,int N,int D){
unsigned int tix = threadIdx.x + blockIdx.x * blockDim.x;
if (tix < N) {
if (tix >= D) {
// -----------------------------------
// ------- Add Partial Results -------
Output[tix] = Input[tix] + Input[tix - D];
}else {
// ----------------------------
// -------- Just Rewrite ------
Output[tix] = Input[tix];
}
}
}As you can see, it is very intuitive. Theoretically, data-rewriting can also be omitted if you are just switching between 2 buffers. It also expects a single – thread dimension. The “D” variable is the distance starting to be 1 in the first iteration and then a power of 2 – 2,4,8 etc. The only problem with this kernel is its huge load on the global memory, which in fact can be up to some extent reduced with an optimized kernel that uses the shared memory:
/**************************************************
*@brief: Optimized Kernel with Shared Memory Usage
**************************************************/
__global__ void Steel_Optimized(int* Global, int N, int Steps) {
unsigned int tx = threadIdx.x;
unsigned int tix = tx + blockIdx.x * blockDim.x;
// ------------------------------------------
// ------- Define Shared Memory Usage -------
__shared__ float Smem[TILE];
// --------------------------------------------
// ------- Load Data from Global Memory -------
Smem[tx] = Global[tix];
__syncthreads();
unsigned int D = 1;
for (int i = 0; i < Steps; i++) {
unsigned int Left = 0;
unsigned int Right = 0;
// ------------------------------------------
// ------- Load To Registers and Sync -------
if (tx >= D) {
Left = Smem[tx - D];
Right = Smem[tx];
}
__syncthreads();
// -------------------------------
// ------- Update and Sync -------
if (tx >= D) {
Smem[tx] = Left + Right;
}
__syncthreads();
// ----------------------------
// ------- update Phase -------
D = D * 2;
}
// --------------------------------------
// ------- Upload Back to Global --------
Global[tix] = Smem[tx];
}This kernel internally loops in steps / phases, which would be in the previous case a loop on the CPU-side. This however has its limits – this kernel is able to do a prefix sum of up to 1024 samples – or more specifically up to a point allowed by CUDA architecture (Keep recommended 1024). Therefore – larger prefix sums must be implemented in a different fashion – most likely by a combination of these two kernels, which is something what I also do call “tiling” – it means to “Do as much work as possible in shared memory and do the rest within global memory” – just as an another example – simple vector sum (Parallel Reduction) or FFT can be also implemented in this fashion.
- The speedup achieved of the shared-memory kernel was 4x on my GTX 1060 (N = 1024)
It is important to note however the __syncthreads(), which are used not just once, but twice and intentionally. The reason is, that we want to load data from shared memory into registers – then synchronize – compute – and then store the data back. But if you omit the second __syncthreads(), it may happen that some threads will start to fetch data from memory which some other threads have not yet updated. Try to un-comment and see what happens ? after all, we all do learn by mistakes.
As always, for the most curious readers, please do find the entire code (Including Host-Code) ➡️ HERE ⬅️ ?