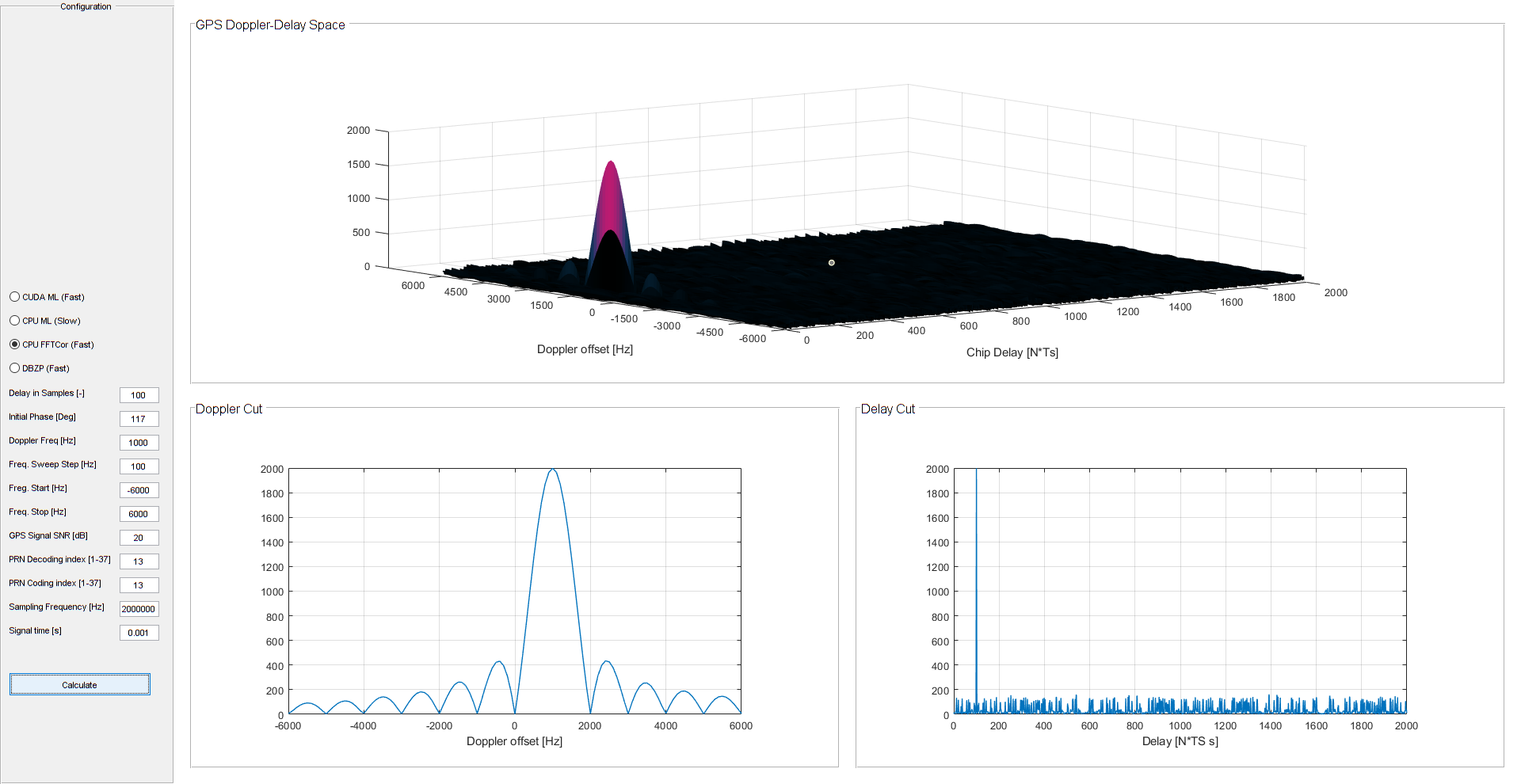
Back in the university, one of my favorite projects I worked on was the estimation of a GPS signal delay and a Doppler Offset. The Doppler offset is simply caused by the fact that GNSS satellites move across the sky while broadcasting on a specified frequency. As a result the final received frequency is different. For L1 (1575.42MHz), the expected range is ~(+-6 KHz). Since the receiver is also interested in the delay between the generated replica and the received signal, it needs to estimate the signal delay. As a result, it basically searches in Time-Frequency space.
In order to find the delay, the receiver basically does autocorrelation with the Satellite’s PRN. Each PRN is a sequence of 1023 samples known as “Gold Codes” used in a GPS system. This is generally known as CDMA (Code Division Multiple Access) – Each GPS satellite uses a dedicated PRN sequence,which is repeated each 1ms (Bitrate of 1.023Mbit/s). GLONASS on the other hand for example uses FDMA (Frequency Division Multiple Access). Below are the most common methods used for the estimation:
- Maximum LikelyHood (ML)
- FFT-Based Correlation
- Double Block Zero Padding (DBZPS)
The least efficient among those is the ML, which calculates an integral for each point in the 2D space. The integration time was however limited to 20ms due to BPSK being used on the signal as well (50bit/s). This modulation is used to broadcast the satellite’s data such as Kepler orbit parameters and trajectory corrections. Later on, the integration time limit has been removed by introduction of the pilot signals without any modulation. The ML is shown below and just for curiosity, my first Matlab implementation took 35 minutes to compute (Doppler Frequency resolution: 100Hz→ 12000/100 = 120(Freq. Res) x 6600 Samples (Time Res) ). Fortunately, this algorithm can be ported to nVidia CUDA very easily and will provide an excellent acceleration as we will see (Still you will likely not find it in commercial receivers).
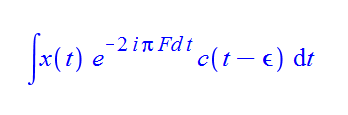
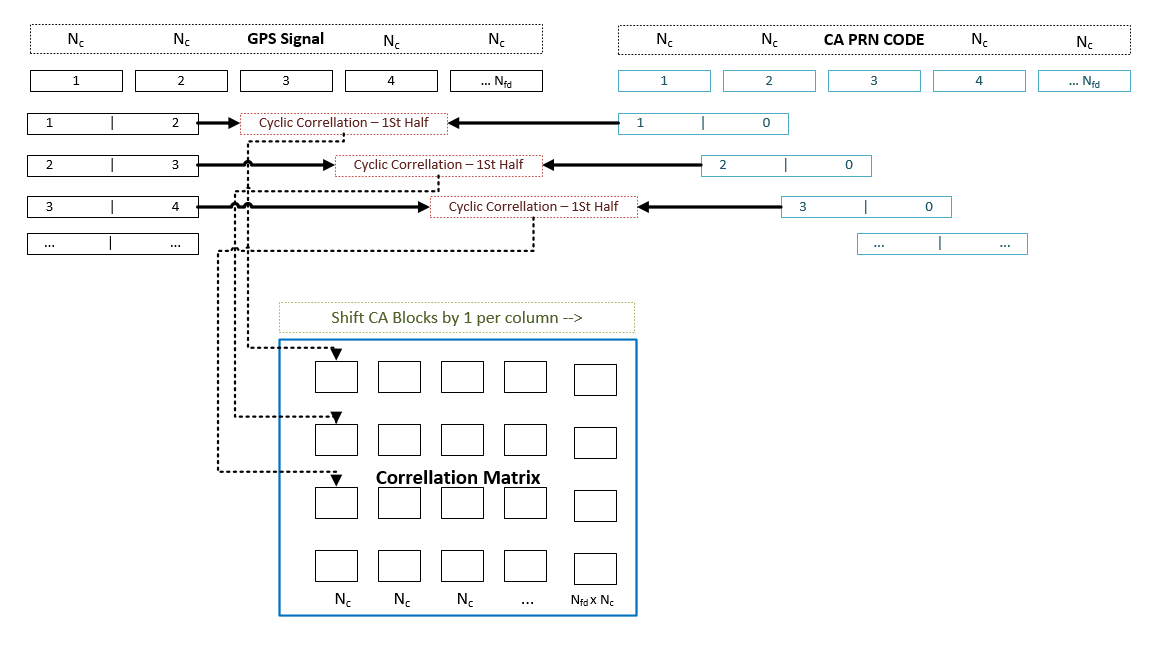
The FFT – Correlation method basically uses FFT algorithm itself as well as the Modulation Property of Fourier Transform – IE. modulating the received signal with a Doppler offset and then computing the autocorrelation via 2 forward and single inverse FFTs. The input signal for DBZP is divided into Nfd blocks of NTc size (Can be specified by user). The same applies for PRN ranging code. While the GPS Signal blocks are padded with another GPS Signal blocks to form a double-sized blocks, the PRN blocks are padded with zeros instead. A cyclic correlation is applied to each of these double-sized blocks and only the first half of the result is left and added to the first column of the final 2D correlation matrix. In the next step, we shift the PRN blocks by 1 (Blocks, not their data!), apply the same operations and fill the second column of the correlation matrix. And so on and on until we fill the whole 2D correlation matrix. In the end a 1D-FFT is applied to each of the columns of the 2D correlation matrix. This method therefore requires plenty of short FFTs:
I have as usual created a simple DEMO – Matlab GUI (Which is not great, but does its job) with all mentioned methods implemented for CPU as well as the ML implemented in CUDA. Feel free to download and compile yourself for your own GPU. Basically the most important part of the code is the ML CUDA Kernel, which is as well as the Julia Fractal Kernel divided into chunk pieces (For the same reason of TDR – Timeout Detection and Recovery). There are also 3 additional scripts:
- Simulation of Satellite Doppler (Basically movement of the Satellite across the sky)
- Position estimation using least squares from multiple satellites (Iterative approach)
- Simulation of Position Error based on Signal’s Multi path properties
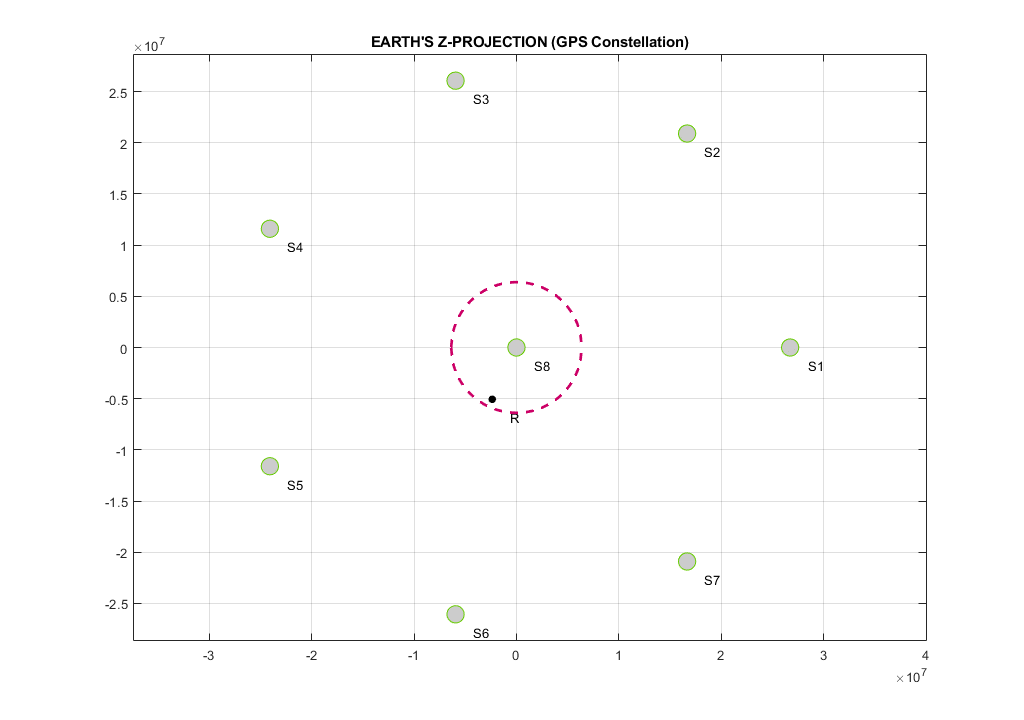

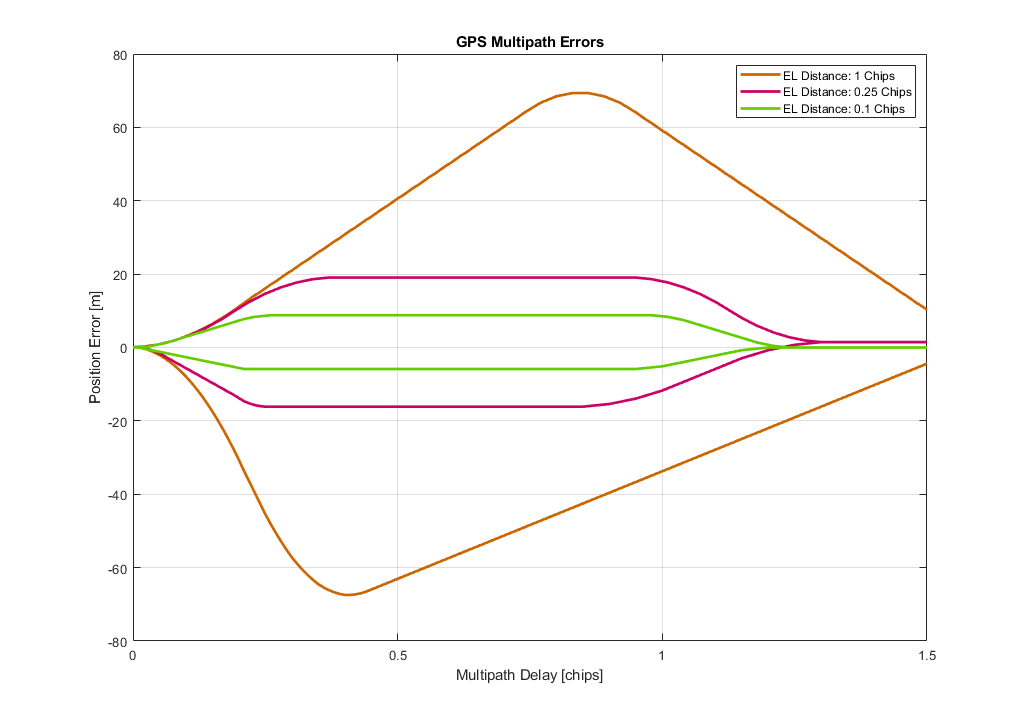
The entire project can be downloaded ➡️ HERE ⬅️ .Note that all the models and/or demos are simplified as much as possible. The satellite constellation used for position estimation is not a real-life scenario (Its custom made,almost perfect). Also the multi path properties will vary especially in the cities. Modern GPS systems use multiple frequencies to negate multi path errors in the ionosphere. The Doppler demo outlines Earth as a sphere and so on. Its basically just to showcase what the GPS / GNSS systems deal with based on mz limited knowledge of those systems.