When I was deciding which topic to use for my diploma thesis back at my university, there were several interesting topics. I ended up choosing “Suppression of photobleaching in Super-Resolution Optical Fluctuation Imaging using digital filtering.” which was kind of close to my specialization and besides, I had a great leader of my thesis. If you are interested, feel free to read HERE . The truth is however that some other topics were of mine own interests as well. One of them particularly was the fast computation of eigenvalues of large matrices, which brought me to writing this post after graduating.
Computing eigenvalues and general linear-algebra tasks on GPU can be quite a funny task for several reasons. First of all, some operations can be quite fast (Now talking about Matrix-Matrix multiply or generic scalar/vector/matrix operations). Some other operations such as vector summation can however exhibit only minor acceleration such as vector summation (So called Parallel Reduction). Can however the famous QR algorithm be implemented also that fast on the GPU? Lets first see how one might compute eigenvalues in a math class:
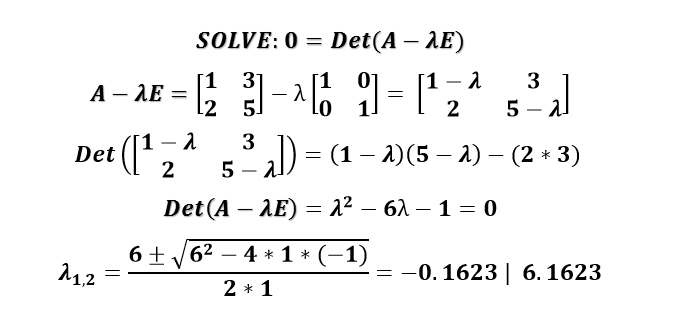
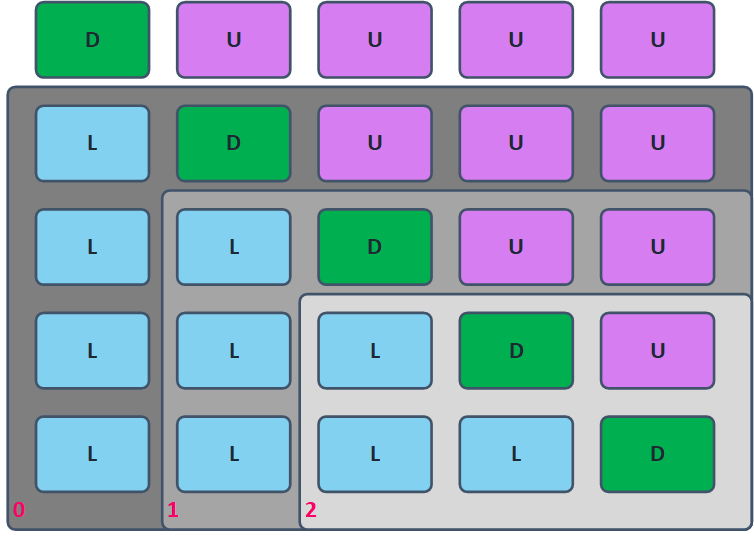
The above example is very straightforward,but things get complicated as the matrix rank increases. Lets start with the standard Linear solver – Gaussian Elimination (Because everybody should be familiar with this method). This method can be implemented into the GPU quite easily. What is however a problem is the underlying algorithm. The reason why I am specifically showing this is that the same scheme can be seen in plenty of other linear solvers and other decomposition algorithms. During first iteration, we eliminate the first column,then second,third and so on. What is however crucial is that while we are progressing, the required “Computing work per stage decreases” – If the matrix is huge, we can launch millions of CUDA threads to do the hard work during stage 1, but as we are finishing the task, we will be launching just a very few threads, which will drastically reduce the performance. See the first 3 steps of this process below:
Good news first – the QR algorithm uses matrix-matrix multiplication. That is a very good start! The bad news is that all other steps are not extra optimal in CUDA. Like Jacobi linear solver,the QR is iterative and within each step, it is necessary to do a QR – Decomposition as shown below with the Gram-Schmidt method. Like all other iterative linear solvers, one might also consider the convergence threshold estimation (Or simply calculate a static amount of iterations). The bad thing about using thresholding is that it requires additional estimations and calculations without really doing the real computing (And as well usually uses summation operation). There are several important things to note:
- Projections from each column are calculated sequentially (IE in order to subtract U2,U1 has to be computed)
- As in the case of Gaussian Elimination,the required workforce reduces over time. For a 1024×1024 matrix, the first iteration is completed with 1023×1024 threads, while the last one uses only 1×1024 threads (Subtract projection from a single column).
- The QR decomposition requires the vector normalization to be used, which includes CUDA – unpopular summations which are semi-fast only.

The Gram-Schmidt decomposition is however not the only one method available. I have implemented the Tri-Diagonalizations with the Given’s rotations and the Hauseholder methods in Matlab (As for the Hauseholder – Also In CUDA). The Given’s rotation method is due to its huge serialization factor not a good candidate for CUDA. The Hauseholder transform unlike the Gram-Schmidt decomposition requires 2 MM-Multiplications, but its my favorite method also due to the fact that its likely the first method, where I do Intentionally launch just one CUDA thread to compute some of the parameters. As a part of the work,I have created a library “QSwift” for some other methods:
- MM MULTIPLY
- Res = QSwiftMatlab(‘IData1′,single(A),’IData2′,single(B),’Type’,’MatrixMatrixMul’);
- GAUSSIAN ELIMINATION
- Res = QSwiftMatlab(‘IData1′,single(A),’Type’,’GaussElim’);
- MATRIX INVERSION
- Res = QSwiftMatlab(‘IData1′,single(A),’Type’,’MatrixInverse’);
- GRAM SCHMIDT DECOMPOSITION
- [Q,R] = QSwiftMatlab(‘IData1′,single(A),’Type’,’GramSchmidt’);
- HAUSEHOLDER TRIDIAGONALIZATION
- Res = QSwiftMatlab(‘IData1′,single(A),’Type’,’HauseHolder’);
- EIGENVALUE SOLVER
- Res = QSwiftMatlab(‘IData1′,single(A),’Precision’,1e-3,’NumIter’,NumIter,’Type’,’Eigenvalues’);
- JACOBI LINEAR SOLVER
- Res = QSwiftMatlab(‘Type’,’Jacobi’,’IData1′,A,’IData2′,B,’NumIter’,NumIter,’Precision’,1e-3);
- SOR LINEAR SOLVER
- Res = QSwiftMatlab(‘Type’,’Sor’,’IData1′, A ,’IData2′, B ,’NumIter’,NumIter,’Omega’,Omega,’Precision’,Precision);
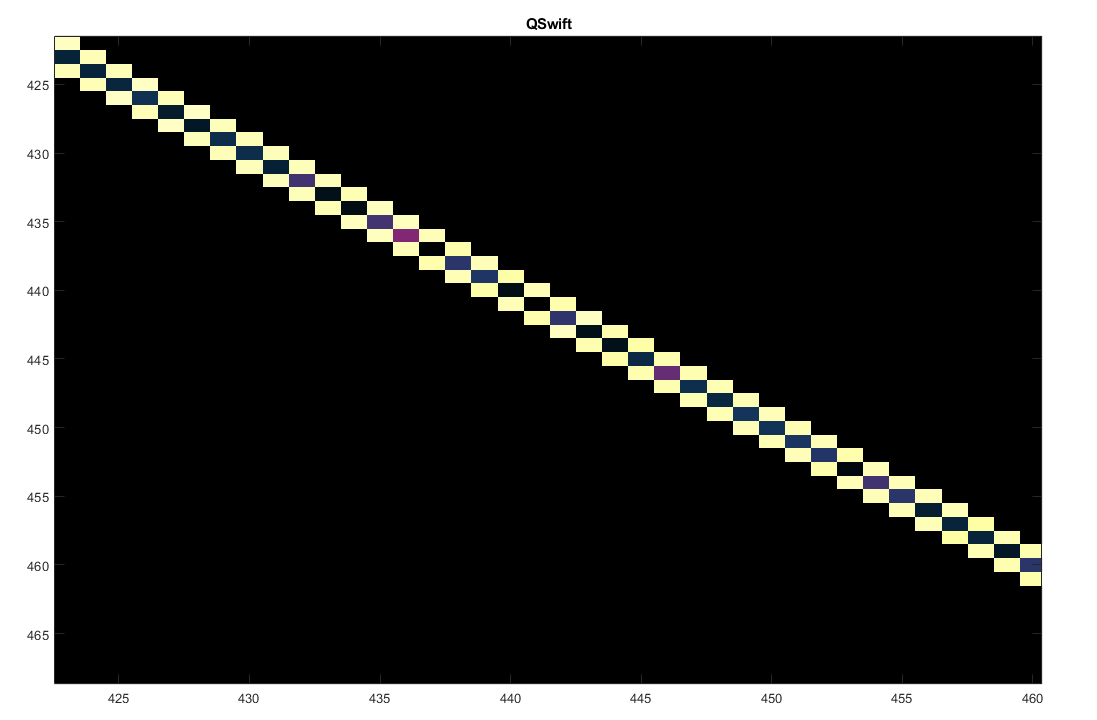
I have compiled the library into 2 parts: The Matlab Part (MEX File) and a QSwift .DLL compiled specifically for VS2019 (X64) and nVidia Pascal Architecture (Compute Capability 6.1). The Matlab part can be linked to any Matlab installation/version and compiled again, however the QSwift DLL is provided “as is” without the sourcecode so far. I may eventually publish those as well. As mentioned previously in one of my posts, the library also uses the nVidia CuBLAS to speedup some of the routines. Please feel free to contact me, should you need some additional information. As a final note: porting the QR algorithm to CUDA architecture is not an easy tasks, requires careful examination of the algorithm and its dependencies. Furthermore, some decomposition algorithms such as the Given’s rotation is not suited to GPU at all.
The Library along its Matlab code routines is shown ➡️ HERE ⬅️ 😇